COUNTING:
-Inventing Numbers
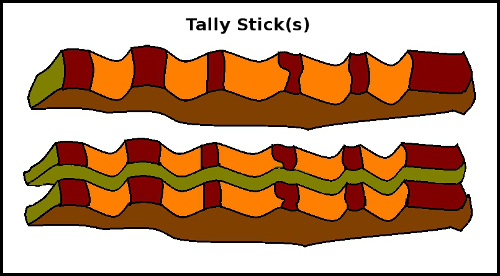
Tally Sticks -Counting without Numbers:
As far as I can see, "Numbers" are created by the process of "Counting".
This may sound silly -but one can "Count" by cutting notches in a stick (for example every time an animal goes into the pen, or a bag of grain is moved from one place to another). One can later slide ones finger from notch to notch and check that the same number of animals ir bags of grain are still present -without actually having to give "names" (like six, seven, etc..) for the numbers.
It is even possible to split the stick in two (or more?) pieces lengthwise -so one has a copy of the tally (a receipt).... All without having to name the "Number" of animals or objects present.....
So, for example, a goat-herder could take the goats out in the morning to forage and bring them home in the evening again -and both the goat-herder and the owner could see that all the goats had returned: Simply by running their thumb along their own stick -without actually knowing how many goats there were.
Perhaps this has conditioned most people into apparently thinking of numbers as a row of numbers stretching off into infinity....
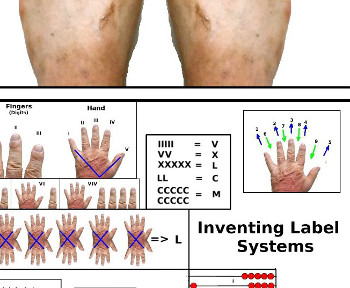
The Human Body as Tally Stick:
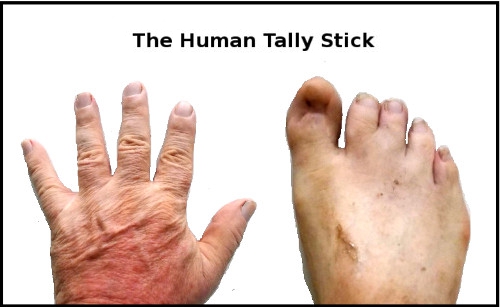
The Human Body is a natural Tally Stick -although not suitable for giving receipts.....
Inventing Names and Concepts:
The Invention of Number
-An Infinite Bag of Balls:
I don't see numbers as a row of numbers stretching off into infinity: Instead, I see myself having a magic bag full of an infinite number of balls. No matter how many balls I take out of the bag -there are always some left in.....
Balls on the Table:

If I have an empty table and take a ball out of the bag and put it on the table -then I have "One" ball.... If I take another ball out and put it on the table -then I have "Two" balls, etc.....
This both creates and solves the problem of knowing how many balls are now on the table.
After a while (around 20 -it seems) we run out of names -so we need a more systematic way of inventing names. The sequence 21, 22, 23, etc... is very clever -because it allows us to "count" any specific number of balls -with no upper limit on the "number" we can count....
Balls in Boxes:
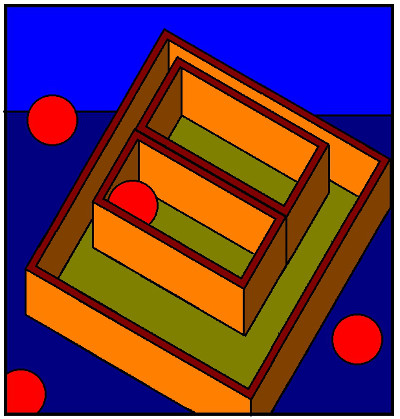
If we really were putting round balls on a flat table -then we would also have a practical problem with most of the balls rolling about all over the table (and possibly falling off)....
So it would be useful if we had a collection of small boxes to put the balls in.
Obviously, it is arbitrary how many balls we put in a box:
However, it would perhaps be a good idea to always put the same number of balls into a box, because then we would know how many balls there were -without having to keep looking in the boxes to see how many balls there were in each of them....
Of course, in real life, this would get a bit messy too, after a while when we have lots of boxes all over the (infinite) table....
So perhaps we need to put the boxes with the balls into bigger boxes -just to keep the table tidy..... We might even have to put boxes containing boxes of balls into larger boxes -as the numbers keep piling up....
Filled and Unfilled Boxes:
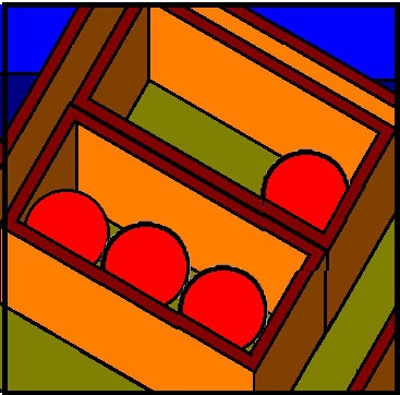
However, when we try to pack the balls away like this -we also discover a few strange things.... For example -suppose we put two balls in every box. After a while we discover that some collections of balls fill up all the boxes -while other collections of balls always leave one box with only one ball in it....
In this case, we would have "discovered" (or invented) "Odd" and "Even" collections.
If we did the same for boxes that contained three -or four -or five (etc.) balls -then we would also invent the concept of "Multiplication" -and any collection of balls could be defined by "the number of boxes" (times) "the number in each box" (plus) any balls left over and not filling a box.
Basically, this is the system underlying Roman Numerals (with 5 balls in a box).....
If we put "ten" balls in each box -then we would have "invented" (or discovered) the "decimal system" (if we invented a symbol which we could put on the box to tell us how many balls were in the box):
So "99" would tell us that we had "nine" boxes with "ten" balls in each and one box left over with "nine" balls in it....
If we then added another ball -we could re-pack the "ten" boxes into a larger box (100) and there would be no boxes with less than ten balls in them....
Blocks, Not Balls:
For convenience, I decided to use blocks instead of balls in the following drawings -but the idea is the same.
The "Numbers" have been colour coded -to make them more recognizable
Base 2:
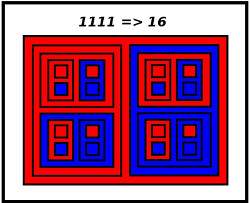
2 Balls in a Box and 2 Boxes in a larger Box
Base 3:
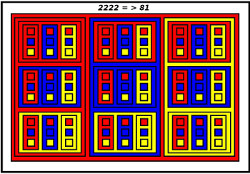
3 Balls in a Box and 3 Boxes in a larger Box
Base 4:
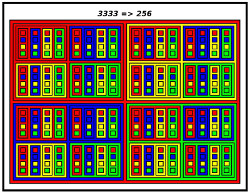
4 Balls in a Box and 4 Boxes in a larger Box
Base 5:
Bases:
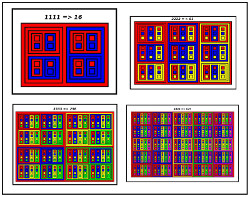
A Summary of the Above
Boxes:
Boxes in Different Shapes and Sizes
-------------------
-------------------